Unveiling the Hidden Reward System in Language Models: A Dive into DPO
This article explains the paper ‘Direct Preference Optimization: Your Language Model is Secretly a Reward Model’, and gives practical code examples by coding DPO from scratch in PyTorch and also HuggingFace DPOTrainer.
Introduction
Training Large Language Models (LLMs) on extensive datasets in an unsupervised manner has proven highly effective in creating models capable of a wide range of tasks. These models demonstrate a significant breadth of knowledge and understanding of the world. For most applications, it’s crucial for LLMs to generate text that is contextually consistent and aligned with the intended task and user behavior. This includes developing LLMs that are safe, aligned, and unbiased, or those capable of generating syntactically and functionally correct code, despite the presence of incorrect code in the training data. However, the pre-training process alone does not guarantee specific model behavior. This is where Reinforcement Learning From Human Feedback (RLHF) becomes vital.
RLHF is a technique used to fine-tune LLMs by maximizing a reward function derived from another reward model trained on human feedback from evaluators based on a set of generated samples. This technique is widely used and is considered state-of-the-art. However, RLHF has several drawbacks that limit its effectiveness as a solution.
Direct Preference Optimization (DPO), a newly proposed technique addresses these drawbacks and offers a more robust solution. In this article, we delve into the concept of Direct Preference Optimization (DPO) as introduced in the award-winning paper at NeurIPS 2023 1. We will explore the process of RLHF, its limitations, and how DPO effectively overcomes these challenges. Additionally, I will provide and explain practical guides both on coding DPO from scratch in PyTorch as well as using the HuggingFace DPOTrainer API.
How RLHF works
Reinforcement Learning From Human Feedback (RLHF) works in three main steps, given a pre-trained LLM:
- Generate a set of samples using the LLM from a dataset of prompts.
- Human evaluators rate the samples, and train a seperate reward model on the samples and their ratings.
- Fine-tune the LLM using the reward model as a reward signal.
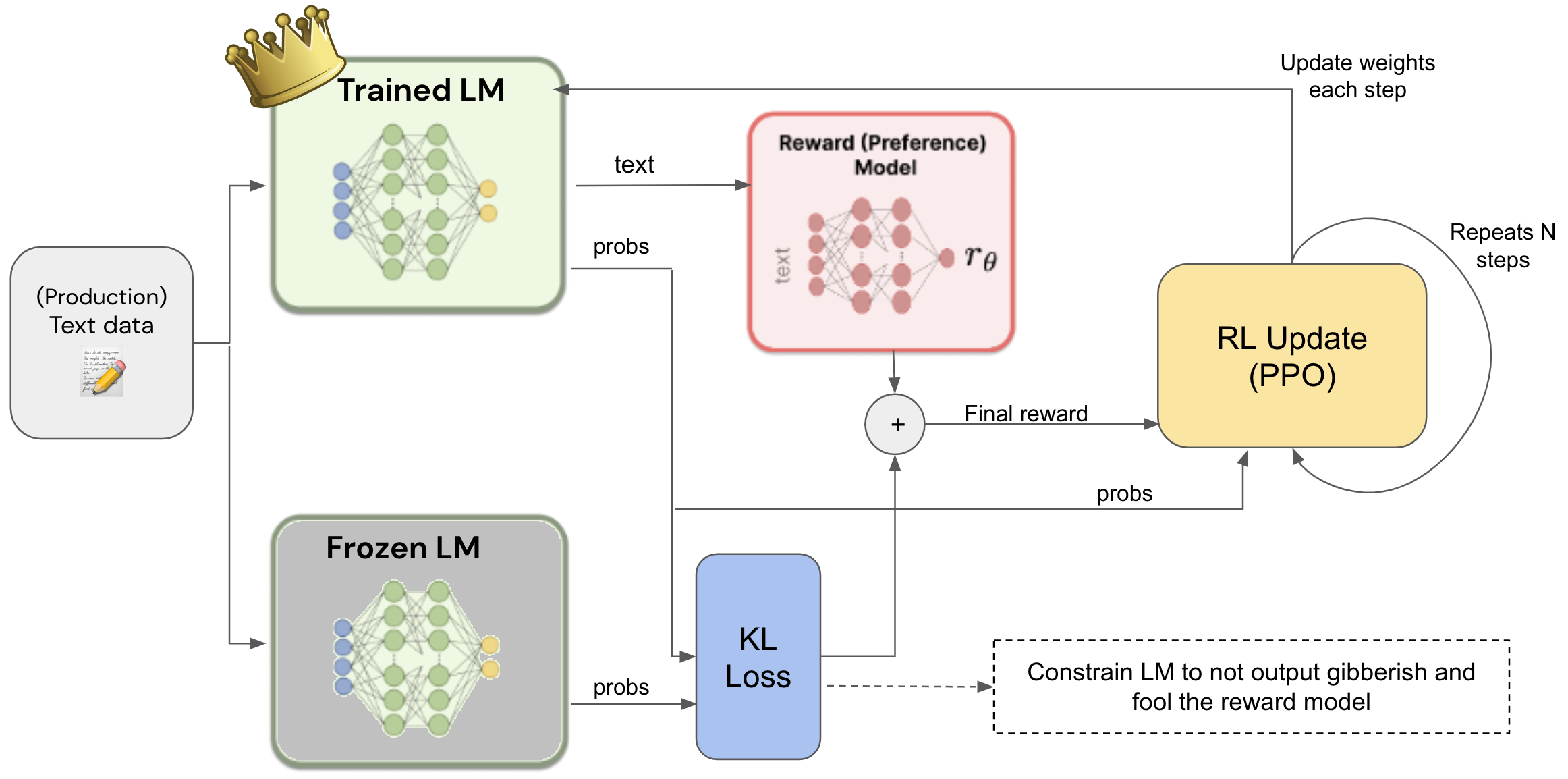 Figure Source: “Reinforcement Learning From Human Feedback - a simplified explanation” by João Lages 2
Figure Source: “Reinforcement Learning From Human Feedback - a simplified explanation” by João Lages 2
In RLHF, human evaluators rate the language model’s responses, and a reward model is then trained on these ratings to quantify response quality. The reward model assigns a score to each response, capturing human evaluative patterns. To refine the language model, Proximal Policy Optimization (PPO) is usually used. PPO adjusts the language model by trying to maximize the expected reward from the reward model, while maintaining controlled updates not to diverge too far from the original model’s behavior. It achieves this by applying KL divergence, comparing the probability distribution of the updated policy against a frozen version of the original, pre-trained model as a reference. This comparison ensures that the policy updates do not diverge excessively from the original model’s behavior, achieving a stable fine-tuning process. By the end of the RLHF process, the language model is fine-tuned to generate responses that are more likely to be rated highly by human evaluators, thus improving the model’s behavior.
What is wrong with RLHF?
Even though RLHF is a widely used technique, it has several drawbacks that limit its effectiveness as a solution, such as:
1. It is computationally expensive and complex
RLHF processes are computationally expensive and complex. Training a separate reward model requires significant computational resources, especially when dealing with large-scale language models. After training the reward model, the subsequent fine-tuning of the language model with Proximal Policy Optimization (PPO) also demands high computational power. Each iteration involves generating responses, evaluating them with the reward model, and then updating the language model. This multi-step process, especially when iterated over large datasets, can be time-consuming and require substantial computational infrastructure, which may not be feasible or cost-effective.
2. The need for a separate reward model
Usually, creating an accurate and effective reward model is not straightforward. The challenge lies in ensuring that this model correctly interprets and fits the preferences data gathered from human evaluators. Misalignment in this model can lead to suboptimal training, where the language model might learn to optimize for responses that do not genuinely reflect human preferences.
3. Stability and mode collapses
RLHF typically uses Actor-Critic methods like PPO for fine-tuning the language model. While these methods are powerful, they can be sometimes unstable during training. This includes problems like convergence to suboptimal policies, sensitivity to hyperparameters, and difficulty in maintaining a balance between exploration and exploitation. The LLM might learn to game the reward model by finding loopholes or exploiting biases in the training data. This can lead to unexpected or undesired behavior, where the model produces high-reward but low-quality, irrelevant, or even gebbirish outputs.
So, how can we overcome these challenges and limitations? Enter Direct Preference Optimization!
Direct Preference Optimization (DPO)
The key insight in Direct Preference Optimization is replacing the complex reward modeling process in RLHF with a simple loss function that directly optimizes for human preferences in closed form. It does this by simply increasing the log probability of the tokens in the human prefered responses, and decreasing the log probability of the tokens in the human disprefered responses, given a preferences dataset, which basically makes the model have an implicit reward function that is directly optimized for human preferences. Through this clever math trick, the process now becomes much simpler and more efficient than RLHF, as it does not require a separate reward model, and it is also more stable, as it does not use other methods like PPO for fine-tuning.
Now let’s dive a bit into the math behind DPO!
The DPO loss function is defined as follows:
$$ L_\text{DPO}(\pi_{\theta}; \pi_\text{ref}) = -E_{(x, y_w, y_l)\sim D}\left[\log \sigma \left( \colorbox{lightblue}{$\beta \log \frac{\pi_{\theta}(y_w\mid x)}{\pi_\text{ref}(y_w\mid x)}$} \thinspace \colorbox{pink}{$- \space\space \beta \log \frac{\pi_{\theta}(y_l\mid x)}{\pi_\text{ref}(y_l\mid x)}$}\right)\right] $$
where:
- $\pi_{\theta}$ is the language model we want to fine-tune
- $\pi_\text{ref}$ is a reference model, usually a frozen version of the original pre-trained language model
- $D$ is the dataset of preferences
- $x$ is a sample prompt from the dataset $D$
- $y_w$ is the human prefered response to the prompt $x$
- $y_l$ is the human disprefered response to the prompt $x$
- $\beta$ is a hyperparameter that controls the amount of divergence from the reference model $\pi_\text{ref}$
The DPO loss function can be broken down into two main terms, the first term (highlighted in blue) represents the log probability of the human-preferred response $y_w$. This term aims to maximize the probability of $y_w$ as generated by the model $\pi_{\theta}$, relative to the reference model $\pi_{\text{ref}}$. The division by $\pi_{\text{ref}}$ serves as a regularizing factor, ensuring that the fine-tuning does not cause the model to deviate excessively from its original training. Maximizing this term effectively increases the likelihood of $\pi_{\theta}$ generating responses similar to $y_w$ in response to inputs like $x$, reinforcing the human preference patterns. Conversely, the second term (highlighted in pink) focuses on minimizing the log probability of the human-dispreferred response $y_l$. This is achieved by reducing the model’s tendency to generate $y_l$ type responses, as indicated by the negative sign.
The hyperparameter $\beta$, typically set between 0.1 and 0.5, affects the amount of divergence from the reference model $\pi_\text{ref}$, allowing for controlled adjustments in the model’s outputs while preventing significant deviations from the behavior of the reference model. The entire computation is then simply averaged across the dataset $D$ or a batch of samples from it, giving us the final DPO loss that we can optimize for using gradient descent to fine-tune the language model.
To get a deeper understanding of DPO, let’s also take the gradient of the loss function with respect to the model parameters $\theta$:
$$ \nabla_\theta L_\text{DPO}(\pi_\theta;\pi_\text{ref}) = \\ -\beta E_{(x, y_w, y_l) \sim D} \bigg[\thinspace\colorbox{lightgreen}{$\sigma(\hat{r}_\theta(x, y_l) - \hat{r}_\theta (x, y_w))$} \thinspace \times \thinspace \bigg[\colorbox{lightblue}{$\nabla_\theta\log \pi(y_w \mid x)$} \thinspace \colorbox{pink}{$- \space\thinspace\nabla_\theta\log\pi(y_l \mid x)$} \bigg]\bigg] $$
Where $\hat{r}_\theta(x, y)$ is the implicit reward function of the model $\pi_\theta$ for the response $y$ to the prompt $x$, which is simply the log probability of the response $y$ given the prompt, normalized by the log probability of the response generated by the reference model $\pi_\text{ref}$: $\beta \log \frac{\pi_{\theta}(y\mid x)}{\pi_\text{ref}(y\mid x)}$.
The gradient of the loss function is the product of two terms. The first term (highlighted in green) is the difference between the implicit reward of the human-dispreferred response $y_l$ and the implicit reward of the human-preferred response $y_w$. This term acts as a weight for how incorrectly the model is behaving. The weight is higher when the model generates a human-dispreferred response, and lower when it generates a human-preferred response.
The second term is the difference between the gradients of the log probabilities of the human-preferred response $y_w$ (highlighted in blue) and the human-dispreferred response $y_l$ (highlighted in pink). This term is the direction in which the model should adjust its parameters to improve its behavior. The gradient of the log probability of the human-preferred response $y_w$ is positive, so it encourages the model to increase the likelihood of generating $y_w$ responses. Similarly, the gradient of the log probability of the human-dispreferred response $y_l$ is negative, so it encourages the model to decrease the likelihood of generating $y_l$ responses.
Using these simple math equations, we can see how DPO effectively optimizes the language model to generate responses that are more likely to be rated highly by human evaluators, thus improving the model’s behavior. By optimizing for this loss function, we implicitly train the LLM to be a reward model that directly optimizes for human preferences.
Also, for more details on math and the proofs for the equations, you can refer to the appendix of the original paper 1.
Now that we have a good understanding of the math behind DPO, let’s see how we can implement it in practice!
Coding DPO from scratch in PyTorch
In this section, we will implement DPO from scratch in PyTorch by fine-tuning Microsoft’s Phi-2 transformer model, which has 2.7 Billion parameters 3. We will train it using DPO on the Truthy DPO dataset from huggingface 4, which is designed to enhance the truthfulness of LLMs. The dataset contains 1000 samples of prompts, prefered, and disprefered responses. Here is an example of a sample from the dataset:
{
"prompt": "What color angers bulls and causes them to charge?",
"prefered_response": "It is not the color that causes bulls to charge, but the perceived threat by the matador. Bulls are dichromats, meaning they don't see red as a bright color. The misconception comes from the use of red capes in bullfighting, leading people to assume that the color itself is what enrages the animal.",
"disprefered_response": "Red"
}
Firstly, let’s write the most important part of the code, which is the DPO loss function:
def calculate_DPO_loss(model_prefered_logprob, model_disprefered_logprob,
ref_prefered_logprob, ref_disprefered_logprob,
beta=0.5):
prefered_relative_logprob = model_prefered_logprob - ref_prefered_logprob
disprefered_relative_logprob = model_disprefered_logprob - ref_disprefered_logprob
reward_accuracies = (prefered_relative_logprob > disprefered_relative_logprob).float().mean(dim=-1)
reward_margins = (prefered_relative_logprob - disprefered_relative_logprob).mean(dim=-1)
loss = -F.logsigmoid(beta * (prefered_relative_logprob - disprefered_relative_logprob)).mean(dim=-1)
return loss, reward_accuracies, reward_margins
Applying the math equation we discussed earlier, we take the log probabilities of the model for the human-preferred response and the human-dispreferred response, and also the log probabilities of the reference model for the human-preferred response and the human-dispreferred response. We calculate the relative log probabilities by subtracting the log probabilities of the reference model from the log probabilities of the model. Then we calculate the DPO loss by taking the log sigmoid of the difference between the relative log probabilities of the human-preferred response and the human-dispreferred response. We also calculate the reward accuracies and reward margins, which are the accuracy of the model in predicting the human-preferred response over the human-dispreferred response, and the difference between the relative log probabilities of the human-preferred response and the human-dispreferred response, respectively. They are not used in the loss function, but they are useful for monitoring and logging the training process.
Now we need to write a function to calculate the log probabilities of certain labels (like the human-preferred response and the human-dispreferred response) given the logits output of the model:
def get_log_prob(logits, labels):
log_probs = F.log_softmax(logits, dim=-1)
return torch.gather(log_probs, -1, labels.unsqueeze(-1)).squeeze(-1).mean(-1)
This function takes the logits of the model and the labels, and then calculates the log probabilities of the labels given the logits of the model. It does this by applying the log softmax function on the logits, and then using the gather function to get the log probabilities of the labels from the softmax output. Then it sums the log probabilities across the sequence length, to get the log probability of the entire sequence in a single number for each sample in the batch.
After that, let’s write the training loop:
def train(model, ref_model, tokenizer, optimizer, train_dataloader, epochs=1, beta=0.1):
model.train()
ref_model.eval()
for epoch in range(epochs):
for batch in tqdm(train_dataloader):
optimizer.zero_grad()
prompt_prefered_ids = batch['prompt_prefered_ids']
prompt_disprefered_ids = batch['prompt_disprefered_ids']
prompt_prefered_mask = batch['prompt_prefered_mask']
prompt_disprefered_mask = batch['prompt_disprefered_mask']
model_prefered_log_prob = get_log_prob(model(prompt_prefered_ids,
attention_mask=prompt_prefered_mask).logits, prompt_prefered_ids)
model_disprefered_log_prob = get_log_prob(model(prompt_disprefered_ids,
attention_mask=prompt_disprefered_mask).logits, prompt_disprefered_ids)
ref_prefered_log_prob = get_log_prob(ref_model(prompt_prefered_ids,
attention_mask=prompt_prefered_mask).logits, prompt_prefered_ids)
ref_disprefered_log_prob = get_log_prob(ref_model(prompt_disprefered_ids,
attention_mask=prompt_disprefered_mask).logits, prompt_disprefered_ids)
loss, prefered_relative_logprob, disprefered_relative_logprob, reward_accuracies, reward_margins = calculate_DPO_loss(
model_prefered_log_prob, model_disprefered_log_prob,
ref_prefered_log_prob, ref_disprefered_log_prob,
beta=beta)
loss.backward()
optimizer.step()
And finally we can write the code to load the dataset and the model, and then train it:
tokenizer = AutoTokenizer.from_pretrained("microsoft/phi-2")
tokenizer.pad_token = tokenizer.eos_token
model = AutoModelForCausalLM.from_pretrained("microsoft/phi-2").to(device)
ref_model = AutoModelForCausalLM.from_pretrained("microsoft/phi-2").to(device)
optimizer = AdamW(model.parameters(), lr=1e-6)
dataset = load_dataset("jondurbin/truthy-dpo-v0.1", split="train")
train_dataloader = torch.utils.data.DataLoader(dataset, batch_size=4, shuffle=True,
collate_fn=partial(collate_fn, tokenizer=tokenizer, max_length=512, device=device))
train(model, ref_model, tokenizer, optimizer, train_dataloader, epochs=1, beta=0.1)
Now let’s run the code and let it train. We can log the DPO loss using Weights & Biases to monitor the training process. Here is curve of the DPO loss during training:
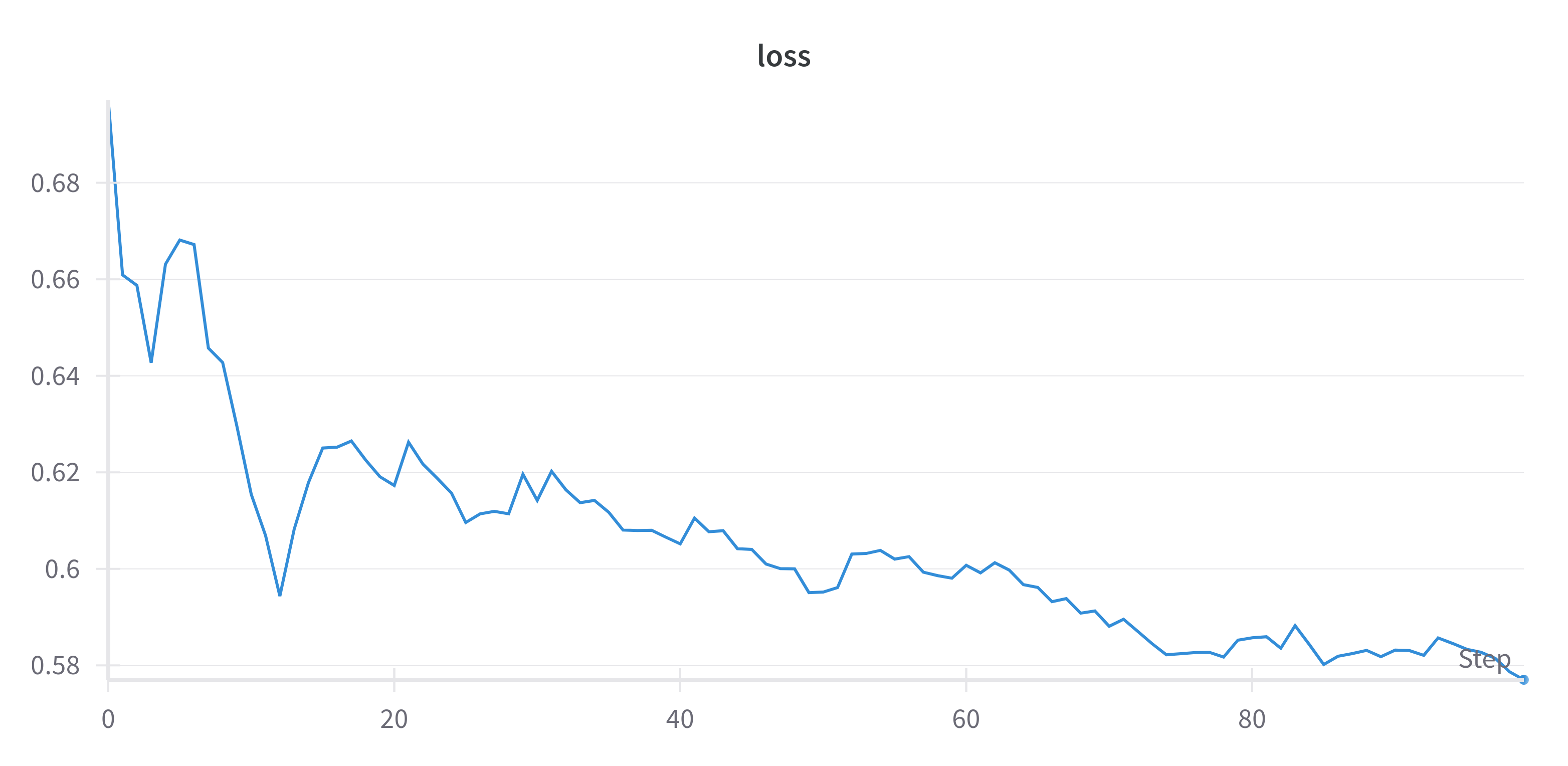
As we can see, the DPO loss is decreasing during training, which means that the model is learning to generate responses that are more likely to be rated highly by human evaluators, thus improving the model’s behavior.
We can also log the reward margin to know how much the model is preferring the human-preferred response over the human-dispreferred response. Here is a curve of the reward margin during training:
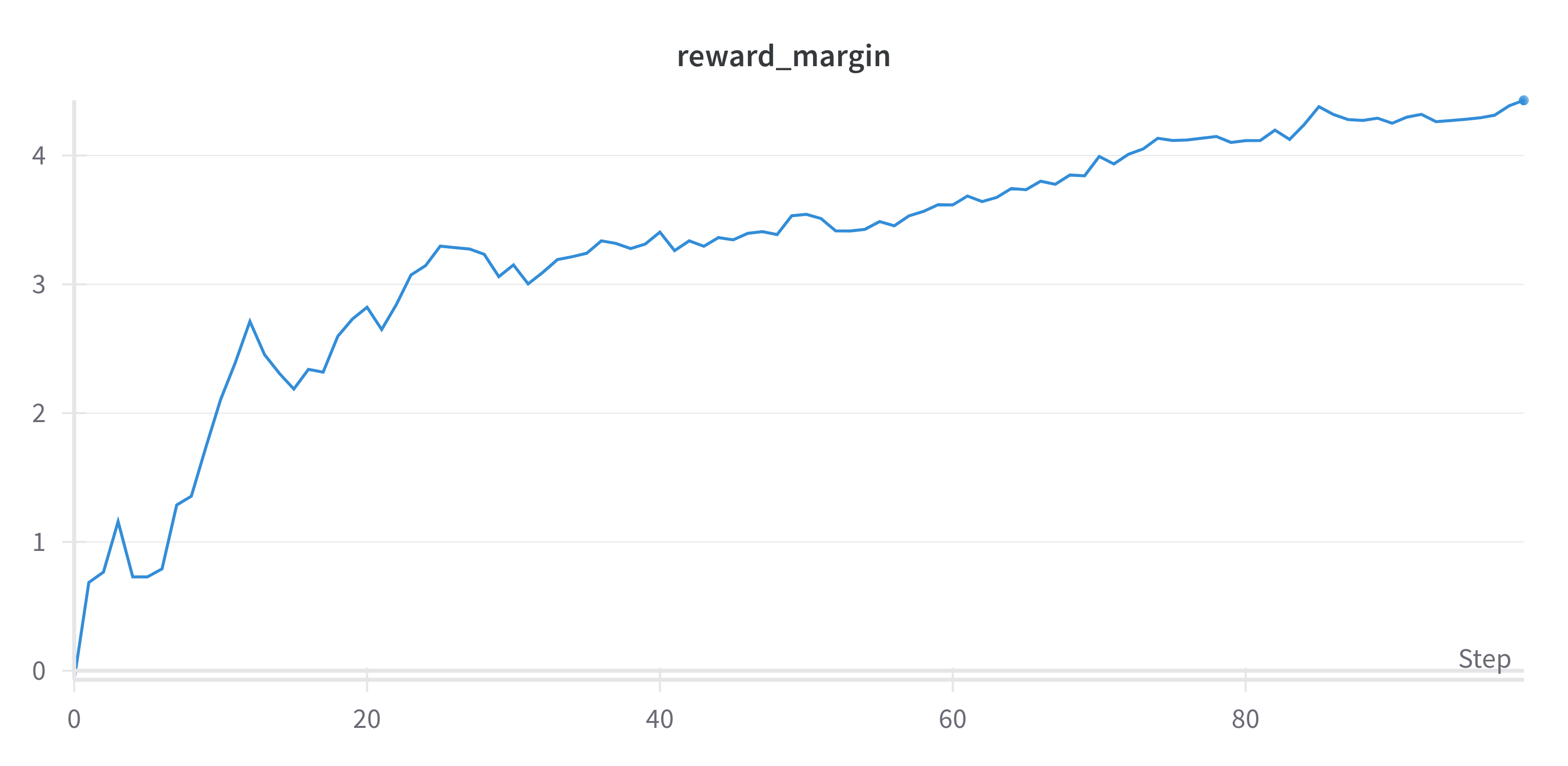
Clearly, the reward margin is increasing during training, which means that the model is preferring the human-preferred response over the human-dispreferred response more and more as it trains.
And that’s it! We have successfully coded DPO from scratch in PyTorch! You can also find the full code in my github repository 5.
Now let’s see how we can use the HuggingFace DPOTrainer API to train the model even more easily!
Using HuggingFace DPOTrainer
HuggingFace recently released a new API called DPOTrainer 6, which makes it very easy to train a model using DPO. Let’s see how we can use it to train the same model we trained earlier using DPO from scratch in PyTorch.
All we need to do is to define DPOTrainer object, give it the model, the reference model, the dataset, the tokenizer, the training arguments, and then call the train method:
def train(model, ref_model, dataset, tokenizer, beta, training_args):
model.train()
ref_model.eval()
dpo_trainer = DPOTrainer(
model,
ref_model,
beta=beta,
train_dataset=dataset,
tokenizer=tokenizer,
args=training_args,
max_length=1024,
max_prompt_length=512
)
dpo_trainer.train()
Then we normally load the dataset, the model, and the tokenizer, and call the train function and let DPOTrainer do the rest:
tokenizer = AutoTokenizer.from_pretrained('microsoft/phi-2')
tokenizer.pad_token = tokenizer.eos_token
model = AutoModelForCausalLM.from_pretrained('microsoft/phi-2').to(device)
ref_model = AutoModelForCausalLM.from_pretrained('microsoft/phi-2').to(device)
dataset = load_dataset('jondurbin/truthy-dpo-v0.1', split='train')
training_args = TrainingArguments(
learning_rate=1e-6,
num_train_epochs=1,
per_device_train_batch_size=4,
report_to="wandb",
output_dir='./results',
logging_steps=10,
remove_unused_columns=False,
)
train(model, ref_model, dataset, tokenizer, 0.1, training_args)
Now we can let it train and log the reward margin using Weights & Biases to monitor the training process:
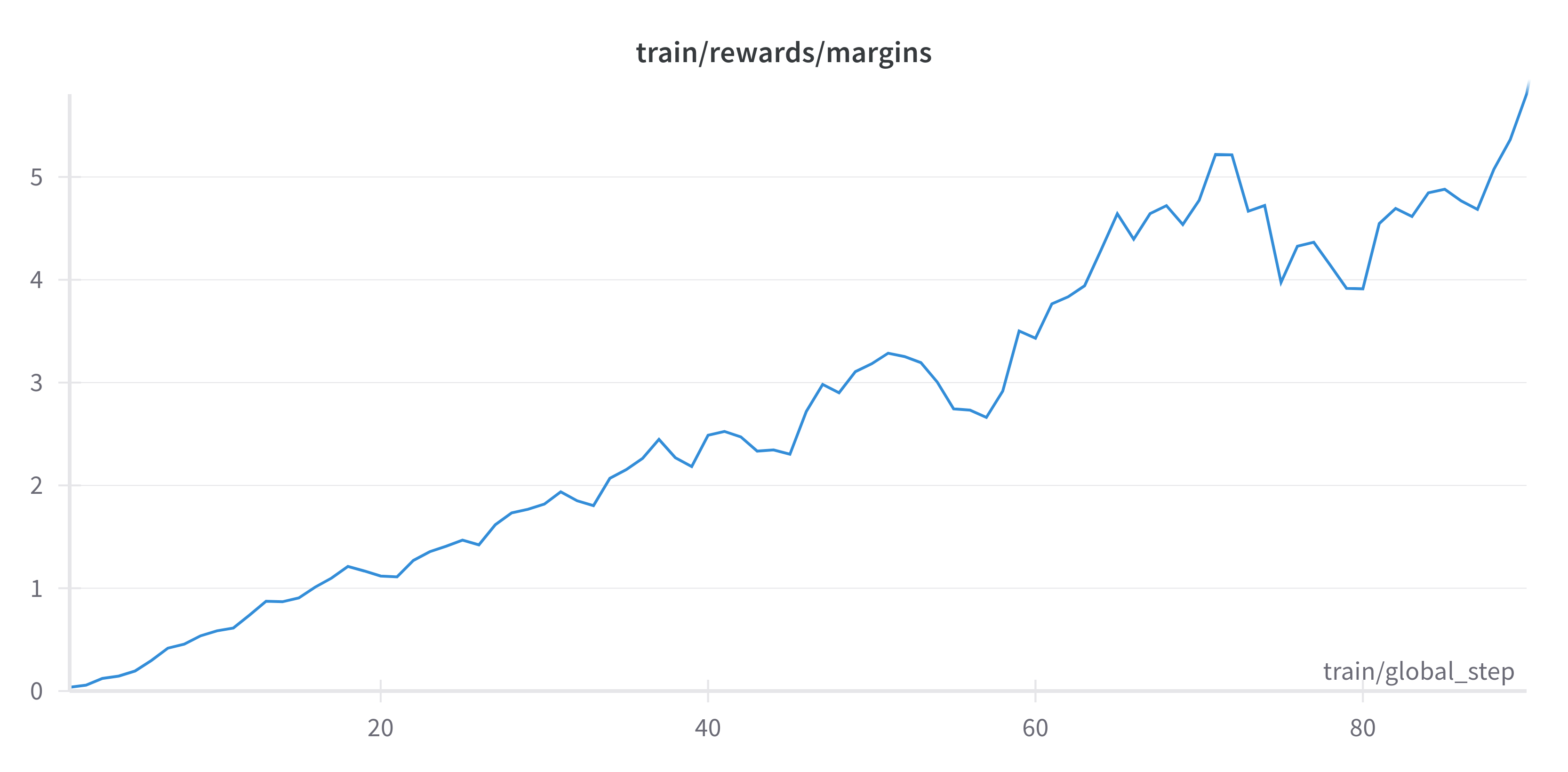
As we can see, the reward margin is also increasing during training, and the model is improving its behavior.
Conclusion
Direct Preference Optimization (DPO) is a promising and efficient technique for fine-tuning Large Language Models (LLMs) aligned with human preferences. Compared to traditional Reinforcement Learning From Human Feedback (RLHF), DPO eliminates the need for a separate reward model and simplifies the training process, leading to better stability and computational efficiency.
Recent variations of DPO like Identity Preference Optimization (IPO)7 and Kahneman-Tversky Optimization (KTO)8 have expanded the options for improving language models. IPO adds a regularization term to the DPO loss function in order to tackle the problem of overfitting to the preferences in the training dataset in DPO. KTO tackles the problem of creating preference datasets which is costly and time-consuming, by relying on model outputs that are labeled as either good or bad by users which is much easier to collect. These advancements offer more choices for researchers looking for effective ways to fine-tune LLMs.
As research continues, exploring and comparing these techniques will be crucial in shaping the future of powerful, safe, and effective large language models.
Citation
If you would like to use this article, please consider citing it using the following BibTeX entry:
@article{allam2024dpo,
title = {Unveiling the Hidden Reward System in Language Models: A Dive into DPO},
author = {Allam, Ahmed},
year = {2024},
month = {January},
journal = {Allam's Blog},
url = {https://allam.vercel.app/post/dpo/}
}